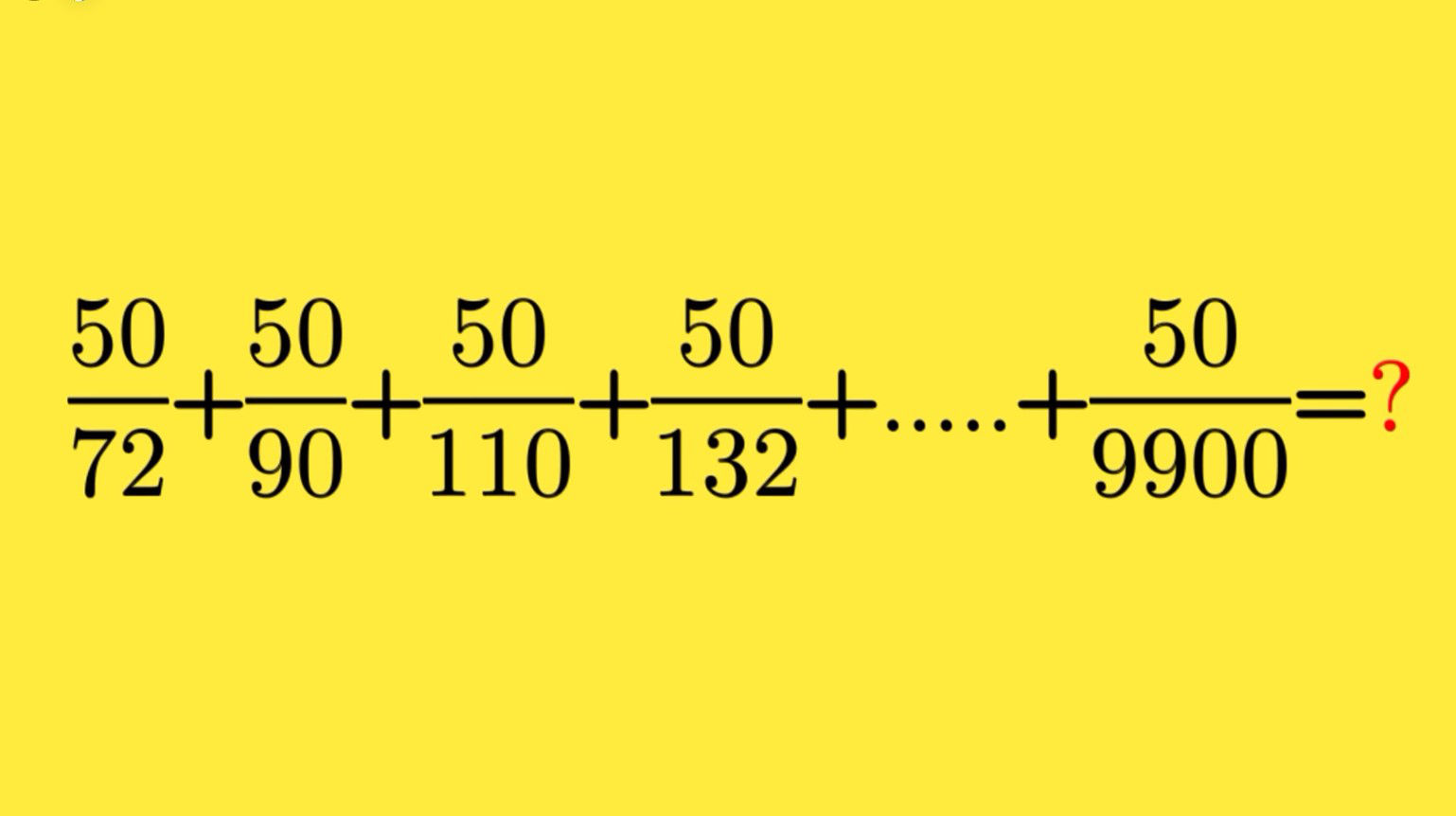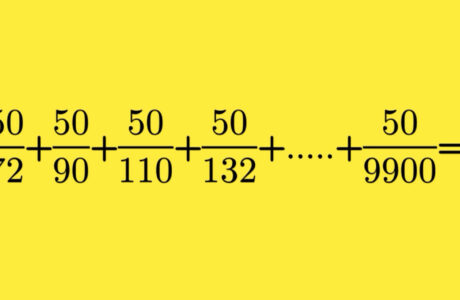Le défi est le suivant : à quel nombre est égal la somme ci-dessous :
|
somme =
|
50
72
|
+
|
50
90
|
+
|
50
110
|
+
|
50
132
|
+
|
…
|
+
|
50
9900
|
= ?
|
Source : https://www.facebook.com/augustomens/videos/1192576432483271/
Étape 1 : mettre en facteur le nombre 50.▲
|
somme =
|
50 (
|
1
72
|
+
|
1
90
|
+
|
1
110
|
+
|
1
132
|
+
|
…
|
+
|
1
9900
|
)
|
Étape 2 : pouvoir se rendre compte que les dénominateurs sont les produits d’entiers successifs.▲
72 = 8 × 9 ; 90 = 9 × 10 ; 110 = 10 × 11 ; 132 = 11 × 12 et… 9900 = 99 × 100.
Donc, en remplaçant les dénominateurs, on peut écrire la somme de la manière suivante :
|
somme =
|
50 (
|
1
8 × 9
|
+
|
1
9 × 10
|
+
|
1
10 × 11
|
+
|
1
11 × 12
|
+
|
…
|
+
|
1
99 × 100
|
)
|
Étape 3 : se rendre compte que l’on peut écrire les fractions autrement.▲
…car, pour toutes les fractions dans cette somme, la somme b – a = 1 (différence de 2 nombres successifs).
|
1
a × b
|
=
|
b – a
a × b
|
=
|
b
a × b
|
–
|
a
a × b
|
=
|
1
a
|
–
|
1
b
|
En remplaçant les fractions par la nouvelle forme :
|
somme =
|
50 (
|
1
8
|
–
|
1
9
|
+
|
1
9
|
–
|
1
10
|
+
|
1
10
|
–
|
1
11
|
+
|
1
11
|
–
|
1
12
|
+
|
…
|
+
|
1
99
|
–
|
1
100
|
)
|
Étape 4 : s’apercevoir que des termes s’éliminent.▲
|
–
|
1
9
|
+
|
1
9
|
= 0
|
||
|
–
|
1
10
|
+
|
1
10
|
= 0
|
||
|
–
|
1
11
|
+
|
1
11
|
= 0
|
||
|
…
|
–
|
1
99
|
+
|
1
99
|
= 0
|
Après élimination des termes, il reste :
|
somme =
|
50 (
|
1
8
|
–
|
1
100
|
)
|
Dernière étape : simplifier au maximum la fraction.▲
|
somme =
|
50 (
|
1
8
|
–
|
1
100
|
)
|
=
|
50 ×
|
100 – 8
800
|
=
|
5 × 46
40
|
=
|
46
8
|
=
|
23
4
|
Résultat final.▲
|
somme =
|
23
4
|
= 5,75
|
Voilà, le calcul est terminé. En fait, selon moi, la difficulté réside dans la faculté de « voir », de « se rendre compte », de pouvoir regarder pour simplifier l’écriture de la somme. Du pouvoir de regarder dans la juste proximité.