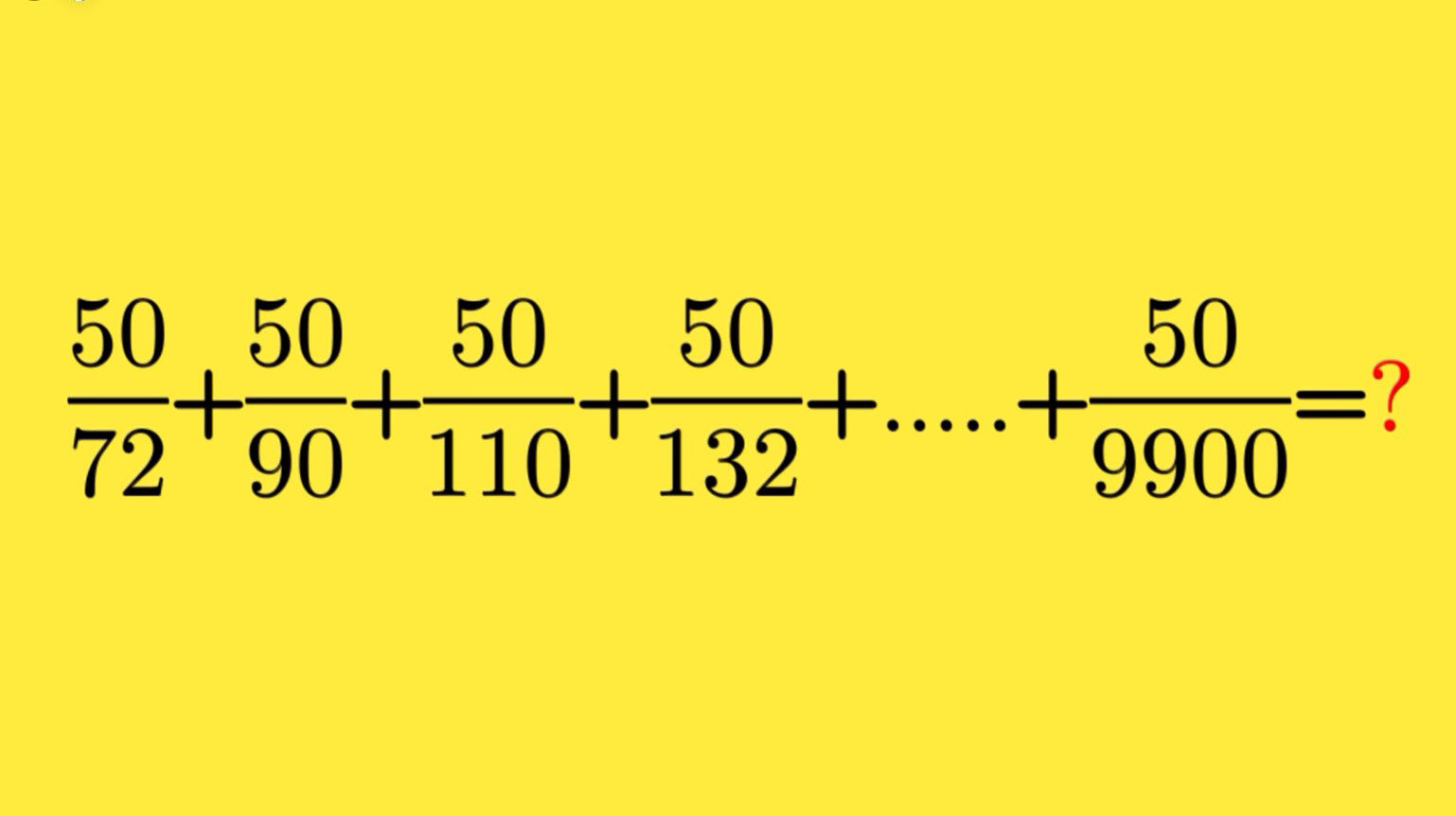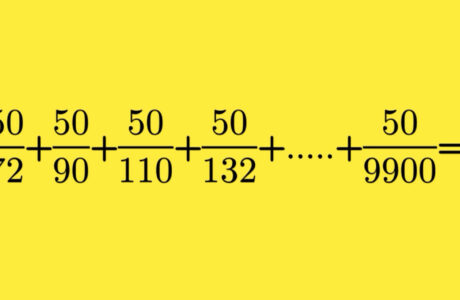The challenge is: what number is the sum below equal to:
|
sum =
|
50
72
|
+
|
50
90
|
+
|
50
110
|
+
|
50
132
|
+
|
…
|
+
|
50
9900
|
= ?
|
Source: https://www.facebook.com/augustomens/videos/1192576432483271/
Step 1: factorize with the number 50.▲
|
sum =
|
50 (
|
1
72
|
+
|
1
90
|
+
|
1
110
|
+
|
1
132
|
+
|
…
|
+
|
1
9900
|
)
|
Step 2: be able to realize that the denominators are the products of successive integers.▲
72 = 8 × 9; 90 = 9 × 10; 110 = 10 × 11; 132 = 11 × 12 and… 9900 = 99 × 100.
So, by replacing the denominators, we can write the sum as follows:
|
sum =
|
50 (
|
1
8 × 9
|
+
|
1
9 × 10
|
+
|
1
10 × 11
|
+
|
1
11 × 12
|
+
|
…
|
+
|
1
99 × 100
|
)
|
Step 3: realize that fractions can be written differently.▲
… because, for all fractions in this sum, the sum b – a = 1.
|
1
a × b
|
=
|
b – a
a × b
|
=
|
b
a × b
|
–
|
a
a × b
|
=
|
1
a
|
–
|
1
b
|
Replacing the fractions with the new form:
|
sum =
|
50 (
|
1
8
|
–
|
1
9
|
+
|
1
9
|
–
|
1
10
|
+
|
1
10
|
–
|
1
11
|
+
|
1
11
|
–
|
1
12
|
+
|
…
|
+
|
1
99
|
–
|
1
100
|
)
|
Step 4: notice that terms are being eliminated.▲
|
–
|
1
9
|
+
|
1
9
|
= 0
|
||
|
–
|
1
10
|
+
|
1
10
|
= 0
|
||
|
–
|
1
11
|
+
|
1
11
|
= 0
|
||
|
…
|
–
|
1
99
|
+
|
1
99
|
= 0
|
After eliminating the terms, there remains:
|
sum =
|
50 (
|
1
8
|
–
|
1
100
|
)
|
Final step: simplify the fraction as much as possible.▲
|
sum =
|
50 (
|
1
8
|
–
|
1
100
|
)
|
=
|
50 ×
|
100 – 8
800
|
=
|
5 × 46
40
|
=
|
46
8
|
=
|
23
4
|
Final result.▲
|
sum =
|
23
4
|
= 5,75
|
So, the calculation is complete. In fact, according to me, the difficulty lies in the ability to “see,” to “realize,” to be able to look in order to simplify the writing of the sum. The power to look in the right proximity.